
Diophantine footy
Last weekend, while watching my son’s footy team (GO BEARS!), my dad noticed that the Bears’ score, 7-7-49, had an unusual property, the score (calculated as 6 times the number of goals \(g\) plus the number of behinds \(b\)) was also the product of the goals and behinds. He posed the question: ‘Are there any other scores that have this property?’ Off the top of my head, it struck me that the score of 0-0-0, also satisfies the equation.
The next day, my dad emails me with two other solutions 4-8-32 and 3-9-27, and posed the question: ‘Are these all the solutions, and how would you prove that you have them all?’ So here it is:
So we are looking for cases when
\begin{align}
6g + b &= gb \\\
\Rightarrow g &= \frac{b}{b - 6}
\end{align}
(where \(g\) is the number of goals and \(b\) is the number of behinds). Note that we need \(g, b \ge 0\) and \(g, b\) whole numbers (hence Diophantine). Also note that we need to have \(2(b-6) \le b \Rightarrow b \le 12\) because otherwise \(g\) would not be a whole number, this limits the number of possible solutions. Also also note that the right hand side has \(b-6\) in the denominator, so for \(g\) to be positive (and finite), we need \(b>6\).
We can therefore proceed by brute-force and check all allowed values of \(b\):
\begin{align}
b = 7, g = \frac{b}{b-6} &= \frac{7}{1} = 7 \\\
b = 8, g = \frac{b}{b-6} &= \frac{8}{2} = 4 \\\
b = 9, g = \frac{b}{b-6} &= \frac{9}{3} = 3 \\\
b = 10, g = \frac{b}{b-6} &= \frac{10}{4} \\\
b = 11, g = \frac{b}{b-6} &= \frac{11}{5} \\\
b = 12, g = \frac{b}{b-6} &= \frac{12}{6} = 2
\end{align}
Which gives us the solutions noted above, plus one new one 2-12-24 (the cases \(b=10,11\) don’t provide us with whole goals). And that’s it. QED :)
Here is a plot of goals versus behinds, where you can see the integer solutions:
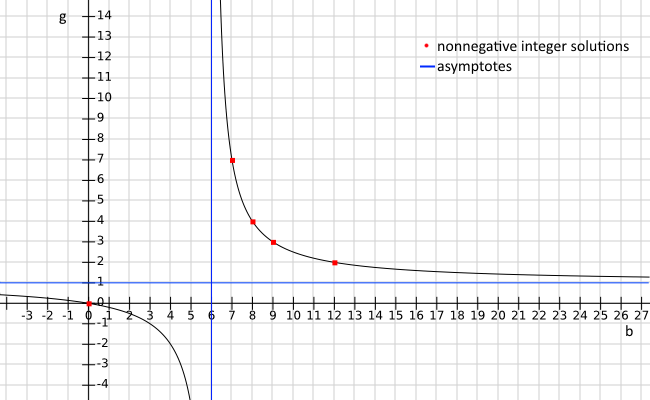
(Bonus: Check out the extra solutions if you allow anti-goals!)
(I think) there are actually a surprising number of solutions here. How would this work out if a goal was worth a different number of points (5, 7, 8, …)?
